En la mayoría de los casos, los parámetros que llegan de los rastreadores tienen un formato fijo y describen un estado específico de la unidad, por lo que pueden ser interpretados inequívocamente por Wialon y mostrados en los mensajes. Sin embargo, algunos rastreadores pueden escribir información de contenido diferente o incluso varios bloques de información en un solo parámetro. En tal caso, para su correcta visualización en Wialon, será necesario configurar el sensor de una manera especial. Para esto, es necesario utilizar el control de parámetros bit a bit, que es de lo que trata este artículo.
Problemática
Existen rastreadores que permiten transmitir parámetros personalizados, cuyo contenido puede variar dependiendo de la configuración del dispositivo.
Por ejemplo, en Wialon puede mostrarse el parámetro user_value = 2646793773, aunque desde el lado del rastreador se pretendía transmitir uno de los siguientes valores:
- 2646793773 — número entero sin signo;
- 56877 y 40386 — varios números enteros;
- −499310125 — número entero con bit de signo;
- −5.15811×10−21 o −0.00000000000000000000515811 — número de punto flotante,
- etc.
Teóricamente, este problema se puede resolver desde el lado de Wialon mediante la modificación del script que analiza los datos que llegan del rastreador. Sin embargo, esto afectaría a todos los usuarios, y ellos pueden tener diferentes configuraciones de rastreadores, es decir, pueden esperar diferentes resultados del análisis de datos por parte del script. Afortunadamente, existe un método para resolver el problema que es adecuado para todos: crear un sensor con la fórmula necesaria. Además, se basará en la representación del parámetro en el sistema binario, ya que ya sabemos que la representación en el sistema decimal puede ser diferente. En forma binaria, el valor del parámetro del ejemplo anterior se escribe de la siguiente manera: 1001 1101 1100 0010 1101 1110 0010 1101. Ahora veamos cómo trabajar con el sistema binario.
Base teórica
En esta sección se examinará la información necesaria para aplicar las fórmulas posteriores.
Sistemas numéricos
En matemáticas se utilizan diferentes sistemas numéricos. Los más familiares para entender son los sistemas numéricos posicionales, en los que el valor de cada dígito depende de su posición. Por ejemplo, en el sistema decimal, el dígito 1, dependiendo de su posición en el número, puede significar una unidad (1), una decena (10), una centena (100) y así sucesivamente.
El número de dígitos utilizados en los sistemas numéricos posicionales se llama base.
En la tabla siguiente se muestran varios sistemas numéricos comunes:
Nombre | Notación | Base | Área de aplicación | Símbolos utilizados |
|---|
Binario | BIN | 2 | Matemática discreta, informática, programación | 0, 1 |
Decimal | DEC | 10 | En todas partes | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Hexadecimal | HEX | 16 | Informática, programación | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Para una rápida conversión de números de un sistema numérico a otro, se puede utilizar la aplicación Calculadora (está preinstalada en cada computadora, o se pueden encontrar sus análogos en Internet) en modo Programador (o similar).
Se puede inventar y usar cualquier sistema numérico, por ejemplo, el sistema de base 13, pero no es de uso común, lo que puede llevar a dificultades al analizar los datos en el lado receptor.
El uso de diferentes sistemas numéricos tiene no solo razones históricas o culturales, sino también fundamentos prácticos. El sistema binario, poco familiar para las personas, simplifica significativamente los cálculos matemáticos para los dispositivos electrónicos. Además, el sistema binario es conveniente desde el punto de vista de la simplicidad de reconocimiento de valores en presencia de ruido, ya que es más fácil distinguir la ausencia de voltaje de su presencia que determinar un nivel específico de voltaje de 0 a 9.
Bits y bytes
Bit es un dígito del código binario.
Byte es un conjunto de 8 bits.
Nibble es un grupo de 4 bits, que corresponde a un símbolo en el sistema hexadecimal.
Para facilitar la percepción, los números binarios a menudo se dividen en nibbles con espacios. Es decir, en lugar de escribir 10011101110000101101111000101101 se usará la escritura 1001 1101 1100 0010 1101 1110 0010 1101.
Números de punto flotante
Un número de punto flotante es una forma exponencial de representar números reales, en la que el número se almacena en forma de mantisa y exponente.
A continuación se muestran varios ejemplos de tales números:
125000 = 1.25 × 105 — aquí la mantisa es 1.25 y el exponente es 5.
0.000000125 = 1.25 × 10−7 — la mantisa es 1.25 y el exponente es −7.
125000000000000 = 1.25 × 1014 — la mantisa es 1.25 y el exponente es 14.
La ventaja de usar tal notación radica en la posibilidad de ampliar significativamente el rango de valores transmitidos mientras se mantiene el número de bits utilizados.
Para representar números de punto flotante en dispositivos digitales, se utiliza más comúnmente el estándar IEEE 754.
Aplicación práctica
En esta sección se examinarán diferentes variantes de parámetros de usuario y fórmulas para su interpretación en Wialon.
Conversión de número binario a decimal entero
Para entender la fórmula de conversión, primero vale la pena mirar los números decimales desde un ángulo un poco inusual. Consideremos el número decimal 125. Consiste en 1 centena, 2 decenas y 5 unidades: 125 = 1 × 100 + 2 × 10 + 5 × 1.
Como ya sabemos, la base del sistema decimal es el número 10. También notemos que las centenas están en el tercer lugar, las decenas en el segundo, las unidades en el primero. Teniendo esto en cuenta, el número se puede representar como la suma de los valores de cada posición, multiplicados por la base del sistema numérico elevada a la potencia igual al número de la posición menos uno:
125 = 1 × 103−1 + 2 × 102−1 + 5 × 101−1 = 1 × 102 + 2 × 101 + 5 × 100
Para calcular un número decimal entero a partir de un número binario, se usa la misma fórmula, pero la base será el número 2: la suma de los bits multiplicados por la base del sistema numérico elevada a la potencia igual al número del bit menos uno.
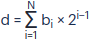
donde d es el número en el sistema decimal, i es el número del bit del número binario, N es el número de bits, bi es el valor del i-ésimo bit.
También esta fórmula se puede presentar de la siguiente manera:
d = bN × 2N−1 + ... + bi × 2i−1 + ... + b2 × 22−1 + b1 × 21−1
Consideremos un ejemplo con el mismo número:
BIN) 0111 1101 = (DEC) 0 × 28−1 + 1 × 27−1 + 1 × 26−1 + 1 × 25−1 + 1 × 24−1 + 1 × 23−1 + 0 × 22−1 + 1 × 21−1 =
= (DEC) 0 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 = (DEC) 26 + 25 + 24 + 23 + 22 + 20 =
= (DEC) 64 + 32 + 16 + 8 + 4 + 1 = (DEC) 125.
Si el valor llega en un parámetro con el nombre user_value, entonces teniendo en cuenta la sintaxis de Wialon, la fórmula tomará la siguiente forma:
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
Este formato de escritura de la fórmula parece más largo, sin embargo, permite rastrear fácilmente la numeración de bits y potencias, lo que permite no cometer errores al escribir la fórmula. Pero si conoce bien las potencias de dos, puede usar una versión simplificada de esta fórmula:
user_value:8*const128+user_value:7*const64+user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+user_value:1*const1
La longitud de la fórmula de conversión dependerá del número de bits considerados, por lo que no será posible copiarla directamente del artículo. Si según el protocolo del rastreador se asigna 1 byte (8 bits) al valor del parámetro, la fórmula será similar a la mostrada arriba (solo será necesario reemplazar el nombre del parámetro en ella). Y si se asignan 3 bytes al parámetro, la fórmula será 3 veces más larga y usará constantes hasta 2^23 = 8388608.
Como se mencionó anteriormente, a veces un solo parámetro puede contener varios valores diferentes. En tal caso, es necesario usar la fórmula dada en la sección anterior, pero considerar solo algunos bits.
Como ejemplo, consideremos el parámetro user_value con el valor (DEC) 32200 = (BIN) 0111 1101 1100 1000. Su primer byte describe el valor del primer contador, y el segundo byte, el valor de otro contador. Es necesario crear dos sensores separados con fórmulas que usarán solo los bytes necesarios.
Parámetro | user_value |
Número de bit del valor original | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Valor del bit | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Número de bit del valor buscado | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Sensor | Contador #2 | Contador #1 |
La fórmula para el primer sensor será similar a la fórmula de la sección anterior, ya que los números de bits del valor original y buscado coinciden:
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
La fórmula para el segundo sensor será diferente, ya que nos referiremos a los bits 9-16, pero los percibiremos como bits 1-8:
user_value:16*const2^const7+user_value:15*const2^const6+user_value:14*const2^const5+user_value:13*const2^const4+user_value:12*const2^const3+user_value:11*const2^const2+user_value:10*const2^const1+user_value:9*const2^const0
Como resultado, de un solo número 32200 podremos obtener:
(BIN) 1100 1000 = (DEC) 200 — valor del primer contador.
(BIN) 0111 1101 = (DEC) 125 — valor del segundo contador.
Consideración del signo del número
En algunos casos, el valor del bit más significativo puede no ser significativo, sino de signo, es decir, contener información no sobre la magnitud del valor, sino sobre si este número es positivo o negativo.
Por ejemplo, si en el parámetro de usuario el rastreador envía el valor 13 o −5, Wialon no lo sabe, y en ambos casos veremos el mismo parámetro user_value = 13, ya que:
(DEC) 13 = (BIN) 1101
(DEC) −5 = (BIN) 1101 — el bit más significativo es responsable del signo menos, y (BIN) 101 = (DEC) 5.
Para interpretar correctamente el bit de signo, es necesario modificar la fórmula de conversión de número binario a decimal entero, agregando al principio −1 elevado a la potencia del bit más significativo:
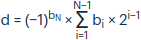
donde d es el número en el sistema decimal, i es el número del bit del número binario, N es el número de bits, bi es el valor del i-ésimo bit.
Esta fórmula también se puede representar de la siguiente manera:
d = (−1)bN × (bN-1 × 2(N−1)−1 + ... + bi × 2i−1 + ... + b2 × 22−1 + b1 × 21−1)
Esta fórmula funciona porque (−1)0 = 1, y (−1)1= −1, lo que permite representar el signo del número con un solo bit.
Si asumimos que el bit de signo es el bit número 32, para tenerlo en cuenta en Wialon es necesario añadir la siguiente fórmula al principio de la expresión en el sensor:
(const-1)^user_value:32*...
Conversión de un número binario a un número decimal de punto flotante
Se trata de la conversión de un número binario normalizado al formato de 32 bits según el estándar IEEE 754. Este estándar no implica la transmisión del número de punto flotante en sí, sino la transmisión de ciertos valores a partir de los cuales se puede calcular el número buscado según la siguiente fórmula:
d = (−1)S × 2(E−127) × (1 + M/223),
donde d es el número en el sistema decimal, S es el signo del número, E es el exponente desplazado, M es el resto de la mantisa normalizada.
Para aplicar esta fórmula no se requiere una comprensión completa de la misma, ya que el estándar describe en qué bits se almacenan S, E y M, que simplemente deben ser sustituidos en la expresión.
Información adicional
En la fórmula proporcionada, no se utiliza el orden del número de punto flotante, que puede ser negativo (por ejemplo, 1.25×10−7), sino el exponente desplazado E, que siempre tiene un valor positivo. El desplazamiento inverso se logra restando 127 del exponente desplazado ya en la fórmula, lo que permite obtener valores negativos.
La mantisa binaria normalizada está en el rango [1; 2), es decir, su primer bit siempre es 1. Por lo tanto, en el estándar IEEE 754 este uno no se envía (ya que se conoce de antemano), sino que se añade en la fórmula en la etapa de cálculo del resultado. Esto permite ahorrar un bit y obtener una mayor precisión del valor transmitido. En la fórmula proporcionada, M no es la mantisa, sino su resto.
Como ejemplo, consideremos el número −5.15811×10−21, que se mostrará en el parámetro como user_value = 2646793773:
(DEC) 2646793773 = (BIN) 1001 1101 1100 0010 1101 1110 0010 1101
Bit de signo (S) | Exponente desplazado (E) | Resto de la mantisa normalizada (M) |
| 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
Según la fórmula de conversión de número binario a decimal entero, obtenemos los valores de M y E.
El resto de la mantisa normalizada M será igual a:
user_value:23*const2^const22+user_value:22*const2^const21+user_value:21*const2^const20+user_value:20*const2^const19+user_value:19*const2^const18+user_value:18*const2^const17+user_value:17*const2^const16+user_value:16*const2^const15+user_value:15*const2^const14+user_value:14*const2^const13+user_value:13*const2^const12+user_value:12*const2^const11+user_value:11*const2^const10+user_value:10*const2^const9+user_value:9*const2^const8+user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
El exponente desplazado E será igual a:
user_value:31*const2^const7+user_value:30*const2^const6+user_value:29*const2^const5+user_value:28*const2^const4+user_value:27*const2^const3+user_value:26*const2^const2+user_value:25*const2^const1+user_value:24*const2^const0
Ahora escribimos la fórmula final teniendo en cuenta la sintaxis de Wialon:
(const-1^user_value:32)*const2^(user_value:31*const2^const7+user_value:30*const2^const6+
user_value:29*const2^const5+user_value:28*const2^const4+user_value:27*const2^const3+
user_value:26*const2^const2+user_value:25*const2^const1+user_value:24*const2^const0-const127)*(const1+
(user_value:23*const2^const22+user_value:22*const2^const21+user_value:21*const2^const20+
user_value:20*const2^const19+user_value:19*const2^const18+user_value:18*const2^const17+
user_value:17*const2^const16+user_value:16*const2^const15+user_value:15*const2^const14+
user_value:14*const2^const13+user_value:13*const2^const12+user_value:12*const2^const11+
user_value:11*const2^const10+user_value:10*const2^const9+user_value:9*const2^const8+
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+
user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+
user_value:2*const2^const1+user_value:1*const2^const0)/const2^const23)
O de forma simplificada:
(const-1^user_value:32)*const2^(user_value:31*const128+user_value:30*const64+user_value:29*const32+
user_value:28*const16+user_value:27*const8+user_value:26*const4+user_value:25*const2+
user_value:24*const1-const127)*(const1+(user_value:23*const4194304+user_value:22*const2097152+
user_value:21*const1048576+user_value:20*const524288+user_value:19*const262144+
user_value:18*const131072+user_value:17*const65536+user_value:16*const32768+user_value:15*const16384+
user_value:14*const8192+user_value:13*const4096+user_value:12*const2048+user_value:11*const1024+
user_value:10*const512+user_value:9*const256+user_value:8*const128+user_value:7*const64+
user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+
user_value:1*const1)/const8388608)
Al sustituir los valores numéricos, obtenemos:
(−1)1 × 2(59−127) × (1 + 4382253/223) = −0.00000000000000000000515811 = −5.15811×10−21
Como podemos ver, el resultado obtenido difiere significativamente del valor inicial del parámetro 2646793773.
Del siguiente bloque puede copiar cómodamente la fórmula para la conversión de un número binario a un número decimal de punto flotante (formato de 32 bits según el estándar IEEE 754):
(const-1^user_value:32)*const2^(user_value:31*const128+user_value:30*const64+user_value:29*const32+user_value:28*const16+user_value:27*const8+user_value:26*const4+user_value:25*const2+user_value:24*const1-const127)*(const1+(user_value:23*const4194304+user_value:22*const2097152+user_value:21*const1048576+user_value:20*const524288+user_value:19*const262144+user_value:18*const131072+user_value:17*const65536+user_value:16*const32768+user_value:15*const16384+user_value:14*const8192+user_value:13*const4096+user_value:12*const2048+user_value:11*const1024+user_value:10*const512+user_value:9*const256+user_value:8*const128+user_value:7*const64+user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+user_value:1*const1)/const8388608)
Oleg Zharkovsky,Customer Service Engineer
2023-05-16