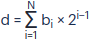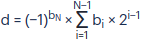В большинстве случаев приходящие от трекеров параметры имеют фиксированный формат и описывают определенное состояние объекта, а потому их можно однозначно интерпретировать со стороны Wialon и отобразить в сообщениях. Однако некоторые трекеры в один параметр могут записывать разную по содержанию информацию или даже несколько блоков информации. В таком случае для ее корректного отображения в Wialon потребуется специальным образом настроить датчик. Для этого необходимо использовать побитовый контроль, о котором и пойдет речь в данной статье.
Проблематика
Существуют трекеры, которые позволяют передавать пользовательские параметры, содержание которых может отличаться в зависимости от конфигурации устройства.
Например, в Wialon может отображаться параметр user_value = 2646793773, хотя со стороны трекера подразумевалась передача одного из следующих значений:
- 2646793773 — целое число без знака;
- 56877 и 40386 — несколько целых чисел;
- −499310125 — целое число со знаковым разрядом;
- −5.15811×10−21 или −0.00000000000000000000515811 — число с плавающей запятой и т. д.
Теоретически данную проблему можно решить со стороны Wialon через изменение скрипта, который разбирает приходящие от трекера данные. Однако это повлияет на всех пользователей, а у них могут быть разные конфигурации трекеров, то есть они могут ожидать разного результата разбора данных со стороны скрипта. К счастью, существует метод решения проблемы, который подойдет для всех, — создание датчика с нужной формулой. При этом основана она будет на представлении параметра в двоичной системе счисления, так как мы уже знаем, что представление в десятичной системе счисления может быть разным. В двоичном виде значение параметра из примера выше записывается следующим образом: 1001 1101 1100 0010 1101 1110 0010 1101. Теперь давайте разберемся, как работать с двоичной системой счисления.
Теоретическая основа
В данном разделе будет рассмотрена информация, необходимая для применения дальнейших формул.
Системы счисления
В математике используются разные системы счисления. Наиболее привычными для понимания являются позиционные системы счисления, в которых значение каждого знака зависит от его позиции (разряда). Например, в рамках десятичной системы цифра 1, в зависимости от позиции в числе, может означать одну единицу (1), один десяток (10), одну сотню (100) и так далее.
Количество знаков, используемых в позиционных системах счисления, называется основанием.
В таблице ниже приведены несколько распространенных систем счисления:
Название | Обозначение | Основание | Область применения | Используемые знаки |
|---|---|---|---|---|
Двоичная (binary) | BIN | 2 | Дискретная математика, информатика, программирование | 0, 1 |
Десятичная (decimal) | DEC | 10 | Повсеместно | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Шестнадцатеричная (hexadecimal) | HEX | 16 | Информатика, программирование | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Для быстрого перевода чисел из одной системы счисления в другую можно использовать приложение Калькулятор (оно предустановлено на каждом компьютере, либо его аналоги можно найти в интернете) в режиме Программист (или аналогичном).
Можно придумать и использовать любую систему счисления, например, тринадцатеричную, но она не является общепринятой, что может привести к трудностям при разборе данных на принимающей стороне.
Использование разных систем счисления имеет не только исторические или культурные причины, но и практические основания. Непривычная людям двоичная система значительно упрощает математические расчеты для электронных устройств. Также двоичная система удобна с точки зрения простоты распознавания значений при наличии шумов, так как отличить отсутствие напряжения от его наличия проще, чем определить конкретный уровень напряжения от 0 до 9.
Биты и байты
Бит — это один разряд двоичного кода.
Байт — это совокупность 8 бит.
Полубайт — это группа из 4 бит, которая соответствуют одному символу в шестнадцатеричной системе счисления.
Для удобства восприятия двоичные числа часто разделяют пробелами на полубайты. То есть вместо записи 10011101110000101101111000101101 будет использоваться запись 1001 1101 1100 0010 1101 1110 0010 1101.
Числа с плавающей запятой
Число с плавающей запятой (или точкой) — это экспоненциальная форма представления действительных чисел, в которой число хранится в виде мантиссы и порядка.
Ниже приведено несколько примеров таких чисел:
125 000 = 1.25 × 105 — здесь мантисса равна 1.25, а порядок равен 5.
0.000000125 = 1.25 × 10−7 — мантисса равна 1.25, а порядок равен −7.
125 000 000 000 000 = 1.25 × 1014 — мантисса равна 1.25, а порядок равен 14.
Преимущество использования подобной записи заключается в возможности значительно расширить диапазон передаваемых значений при сохранении количества задействованных битов.
Для представления чисел с плавающей запятой в цифровых устройствах наиболее часто используется стандарт IEEE 754.
Практическое применение
В данном разделе будут рассмотрены разные варианты пользовательских параметров и формулы для их интерпретации в Wialon.
Преобразование двоичного числа в целое десятичное
Для понимания формулы преобразования стоит сперва взглянуть на десятичные числа под немного непривычным углом. Рассматривать будем десятичное число 125. Оно состоит из 1 сотни, 2 десятков и 5 единиц: 125 = 1 × 100 + 2 × 10 + 5 × 1.
Как мы уже знаем, основанием десятичной системы является число 10. Также зафиксируем, что сотни находятся в третьем разряде, десятки — во втором, единицы — в первом. С учетом этого число можно представить, как сумму значений из каждого разряда, умноженных на основание системы счисления в степени, равной номеру разряда минус один:
125 = 1 × 103−1 + 2 × 102−1 + 5 × 101−1 = 1 × 102 + 2 × 101 + 5 × 100
Для вычисления целого десятичного числа из двоичного используется такая же формула, но основанием уже будет число 2: сумма битов, умноженных на основание системы счисления в степени, равной номеру бита минус один.
,
где d — число в десятичной системе счисления, i — номер бита двоичного числа, N — количество битов, bi — значение i-го бита.
Также эту формулу можно представить в следующем виде:
d = bN × 2N−1 + ... + bi × 2i−1 + ... + b2 × 22−1 + b1 × 21−1
Рассмотрим пример с тем же числом:
(BIN) 0111 1101 = (DEC) 0 × 28−1 + 1 × 27−1 + 1 × 26−1 + 1 × 25−1 + 1 × 24−1 + 1 × 23−1 + 0 × 22−1 + 1 × 21−1 =
= (DEC) 0 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 = (DEC) 26 + 25 + 24 + 23 + 22 + 20 =
= (DEC) 64 + 32 + 16 + 8 + 4 + 1 = (DEC) 125.
Если значение приходит в параметре с именем user_value, то с учетом синтаксиса Wialon формула примет следующий вид:
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
Такой формат записи формулы кажется более длинным, однако он позволяет легко отследить нумерацию битов и степеней, что позволяет не ошибится при записи формулы. Но если вы хорошо знаете степени двойки, то вам может подойти упрощенный вариант данной формулы:
user_value:8*const128+user_value:7*const64+user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+user_value:1*const1
Длина формулы преобразования будет зависеть от количества учитываемых битов, поэтому копировать ее напрямую из статьи не получится. Если по протоколу трекера на значение параметра выделен 1 байт (8 битов), то формула будет аналогична приведенной выше (необходимо будет лишь заменить в ней имя параметра). А если на параметр выделено 3 байта, то формула будет в 3 раза длиннее, и в ней будут использоваться константы вплоть до 223 = 8388608.
Выделение части параметра
Как было отмечено ранее, иногда в одном параметре может содержаться сразу несколько разных значений. В таком случае необходимо использовать формулу, приведенную в предыдущем разделе, однако учитывать только некоторые биты.
В качестве примера рассмотрим параметр user_value со значением (DEC) 32200 = (BIN) 0111 1101 1100 1000. Его первый байт описывает значение первого счетчика, а второй байт — значение другого счетчика. Необходимо создать два отдельных датчика с формулами, которые будут использовать только нужные байты.
| Параметр | user_value | |||||||||||||||
| Номер бита исходного значения | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Значение бита | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| Номер бита искомого значения | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Датчик | Счетчик №2 | Счетчик №1 | ||||||||||||||
Формула для первого датчика будет аналогична формуле из предыдущего раздела, так как номера битов исходного и искомого значения совпадают:
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
Формула для второго датчика будет отличаться, так как мы будем обращаться к битам 9-16, но воспринимать их как биты 1-8:
user_value:16*const2^const7+user_value:15*const2^const6+user_value:14*const2^const5+user_value:13*const2^const4+user_value:12*const2^const3+user_value:11*const2^const2+user_value:10*const2^const1+user_value:9*const2^const0
В итоге из одного числа 32200 мы сможем получить:
(BIN) 1100 1000 = (DEC) 200 — значение первого счетчика.
(BIN) 0111 1101 = (DEC) 125 — значение второго счетчика.
Учет знака числа
В некоторых случаях значение старшего бита может быть не значащим, а знаковым, то есть содержать информацию не о величине значения, а о том, положительное ли это число или отрицательное.
Например, если в пользовательском параметре трекер отправляет значение 13 или −5, то Wialon об этом не знает, и в обоих случаях мы увидим одинаковый параметр user_value = 13, так как:
(DEC) 13 = (BIN) 1101
(DEC) −5 = (BIN) 1101 — старший бит отвечает за минус, а (BIN) 101 = (DEC) 5.
Чтобы интерпретировать знаковый бит правильно, необходимо изменить формулу преобразование двоичного числа в целое десятичное, добавив к ней в начале −1 в степени старшего бита:
,
где d — число в десятичной системе счисления, i — номер бита двоичного числа, N — количество битов, bi — значение i-го бита.
Также эту формулу можно представить в следующем виде:
d = (−1)bN × (bN-1 × 2(N−1)−1 + ... + bi × 2i−1 + ... + b2 × 22−1 + b1 × 21−1)
Данная формула работает, так как (−1)0 = 1, а (−1)1 = −1, что и позволяет отобразить знак числа с помощью одного бита.
Если предположить, что знаковым битом является бит номер 32, то для его учета в Wialon нужно дописать в датчике в начало выражения следующую формулу:
(const-1)^user_value:32*...
Преобразование двоичного числа в десятичное число с плавающей запятой
Речь идет про преобразование двоичного нормализованного числа в 32-битный формат по стандарту IEEE 754. Данный стандарт подразумевает не передачу самого числа с плавающей запятой, а передачу некоторых значений, по которым искомое число можно рассчитать по следующей формуле:
d = (−1)S × 2(E−127) × (1 + M/223),
где d — число в десятичной системе счисления, S — знак числа, E — смещенная экспонента, M — остаток нормализованной мантиссы.
Для применения этой формулы не требуется ее полное понимание, так как в стандарте описано, в каких битах хранятся S, E и M, которые нужно просто подставить в выражение.
В качестве примера рассмотрим число −5.15811×10−21, которое будет отображаться в параметре как user_value = 2646793773:
(DEC) 2646793773 = (BIN) 1001 1101 1100 0010 1101 1110 0010 1101
| Знаковый бит (S) | Смещенная экспонента (E) | Остаток нормализованной мантиссы (M) | |||||||||||||||||||||||||||||
| 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
По формуле преобразования двоичного числа в целое десятичное получаем значения M и E.
Остаток нормализованной мантиссы M будет равен:
user_value:23*const2^const22+user_value:22*const2^const21+user_value:21*const2^const20+user_value:20*const2^const19+user_value:19*const2^const18+user_value:18*const2^const17+user_value:17*const2^const16+user_value:16*const2^const15+user_value:15*const2^const14+user_value:14*const2^const13+user_value:13*const2^const12+user_value:12*const2^const11+user_value:11*const2^const10+user_value:10*const2^const9+user_value:9*const2^const8+user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+user_value:2*const2^const1+user_value:1*const2^const0
Смещенная экспонента E будет равна:
user_value:31*const2^const7+user_value:30*const2^const6+user_value:29*const2^const5+user_value:28*const2^const4+user_value:27*const2^const3+user_value:26*const2^const2+user_value:25*const2^const1+user_value:24*const2^const0
Теперь запишем конечную формулу с учетом синтаксиса Wialon:
(const-1^user_value:32)*const2^(user_value:31*const2^const7+user_value:30*const2^const6+
user_value:29*const2^const5+user_value:28*const2^const4+user_value:27*const2^const3+
user_value:26*const2^const2+user_value:25*const2^const1+user_value:24*const2^const0-const127)*(const1+
(user_value:23*const2^const22+user_value:22*const2^const21+user_value:21*const2^const20+
user_value:20*const2^const19+user_value:19*const2^const18+user_value:18*const2^const17+
user_value:17*const2^const16+user_value:16*const2^const15+user_value:15*const2^const14+
user_value:14*const2^const13+user_value:13*const2^const12+user_value:12*const2^const11+
user_value:11*const2^const10+user_value:10*const2^const9+user_value:9*const2^const8+
user_value:8*const2^const7+user_value:7*const2^const6+user_value:6*const2^const5+
user_value:5*const2^const4+user_value:4*const2^const3+user_value:3*const2^const2+
user_value:2*const2^const1+user_value:1*const2^const0)/const2^const23)
Или упрощенно:
(const-1^user_value:32)*const2^(user_value:31*const128+user_value:30*const64+user_value:29*const32+
user_value:28*const16+user_value:27*const8+user_value:26*const4+user_value:25*const2+
user_value:24*const1-const127)*(const1+(user_value:23*const4194304+user_value:22*const2097152+
user_value:21*const1048576+user_value:20*const524288+user_value:19*const262144+
user_value:18*const131072+user_value:17*const65536+user_value:16*const32768+user_value:15*const16384+
user_value:14*const8192+user_value:13*const4096+user_value:12*const2048+user_value:11*const1024+
user_value:10*const512+user_value:9*const256+user_value:8*const128+user_value:7*const64+
user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+
user_value:1*const1)/const8388608)
При подстановке числовых значений получаем:
(−1)1 × 2(59−127) × (1 + 4382253/223) = −0.00000000000000000000515811 = −5.15811×10−21
Как видим, полученный результат значительно отличается от исходного значения параметра 2646793773.
Из следующего блока вы можете удобно скопировать формулу для преобразование двоичного числа в десятичное число с плавающей запятой (32-битный формат по стандарту IEEE 754):
(const-1^user_value:32)*const2^(user_value:31*const128+user_value:30*const64+user_value:29*const32+user_value:28*const16+user_value:27*const8+user_value:26*const4+user_value:25*const2+user_value:24*const1-const127)*(const1+(user_value:23*const4194304+user_value:22*const2097152+user_value:21*const1048576+user_value:20*const524288+user_value:19*const262144+user_value:18*const131072+user_value:17*const65536+user_value:16*const32768+user_value:15*const16384+user_value:14*const8192+user_value:13*const4096+user_value:12*const2048+user_value:11*const1024+user_value:10*const512+user_value:9*const256+user_value:8*const128+user_value:7*const64+user_value:6*const32+user_value:5*const16+user_value:4*const8+user_value:3*const4+user_value:2*const2+user_value:1*const1)/const8388608)