One of the first and crucial stages of working with Wialon is setting up sensors in the unit. If the sensors are set up correctly, then some standard algorithms will give more accurate results and you will get access to functionality that has not been available before. The calculation table, a tool from the tab of the same name, is considered in detail in this article since this exact tool most often causes difficulties when setting up sensors.

General principle of sensors operation

Wialon supports many types of trackers; you can find their current number on the wialon.com website in the Hardware section. Each of the trackers "speaks" in its own way. Therefore, the parameters which come from different types of trackers and which are displayed on the Messages tab may contain the same information (for example, about temperature or mileage) but have different names. It is necessary to create sensors for each unit in Wialon to prevent users from noticing the differences when using units with various trackers. Also, sensors have a specific type, which allows the system to understand which algorithm to choose to process input values.

However, a simple selection of a sensor type and specifying a parameter in it is often not enough because the parameter value comes in an unobvious to the user way. For example, temp=125 could mean 125°F, 125°C, 12.5°C, or even -3°C. There are three methods to convert the input parameter to the desired type:

1. Expression in the Parameter field;
2. Calculation table;
3. Validation.

They can be used individually or combined. If you use several methods simultaneously, they will be applied in the exact order they are listed above.

Schematically, the use of sensors can be represented as follows:

• The sensor connected to the tracker measures some physical quantity; let’s denote it by S.
• The sensor converts this value and transmits it to the tracker. The X parameter comes from the tracker to Wialon.
  
• Based on the parameter, a sensor is created in Wialon. Then, f(X) transformations are applied to the parameter in the sensor to obtain a human-readable Y value.
  
• Ideally, after transformations in the sensor, the value Y=f(X) should be equal to the value S measured in the first stage. Further, Y will be used in tooltips, reports, notifications, and other Wialon functionality.
  

Since this article only explains the process of setting up the calculation table in Wialon, we will pay attention only to the following elements from the scheme above:

When to use a calculation table

Usually, the calculation table is used in cases where it is necessary to convert the input parameter. However, all three methods mentioned above serve to do this. In what scenario is it worth choosing the calculation table?

In terms of practical application, the calculation table might be used for:

• the calibration table (for example, for weight sensors or fuel level sensors);
  
  
• digital sensors based on analog input data (for example, ignition sensors based on voltage);
  
  
• sensors based on codes that describe different states but come in one parameter (for example, device_status=4 means the ignition is on, and device_status=13 means the panic button is pressed, etc.);
  
  
• sensors that should display positive and negative values, although the parameter associated with them has only positive values (for example, for temperature sensors);
  
  
• any sensors in which it is necessary to separate the range of correct and erroneous values (for example, if the sensor sends specific values in a parameter that indicate errors).

Calculation table settings

The calculation table involves working with the simplest linear functions. That means that the calculation table converts the data in accordance with the Y=a⋅X+b formula — one of the variants of the straight-line equation.

If you understand how each component of this equation works, you can implement valuable and unusual solutions with its help. Next, we will review each area of the Calculation Table tab separately and visualize its impact on the result using a chart.

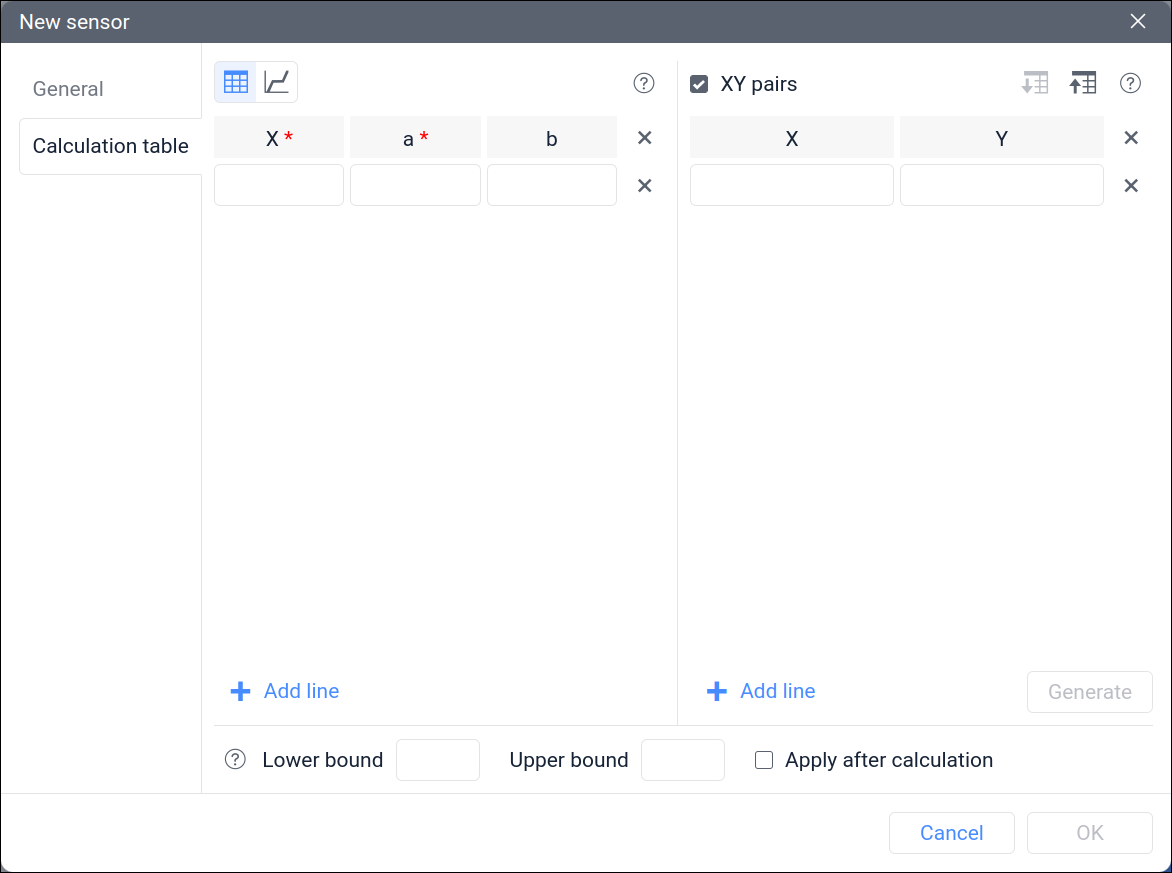
XY pairs

On the right side, you can see the XY pairs block. Filling it in is not enough for the calculation table to work, but it can simplify its settings.

You can add pairs manually or by importing CSV or TXT files (export is available in CSV only). After filling in all the fields of this block, you must click the Generate button (meaning, generate a calculation table based on XY pairs). This action will lead to the values of X, a, and b calculation in the left part of the window.

Each of the added XY pairs corresponds to a point on the chart. As you know, you can draw a line through two points. Therefore, if you enter five XY pairs, you will get four straight lines on the chart.

X is an input value

The central block of the Calculation Table tab contains rows with X, a, and b values. Each of the rows corresponds to a straight line on the chart. The value of X in each row means the beginning of a new straight line, that is, it sets the interval where new values of a and b will be used.

As an example, consider a table with the following values:

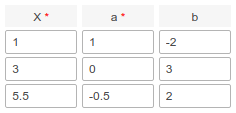
Otherwise, this condition can be written as follows:

• From −∞ to 3 (not including), the equation Y=1⋅X-2 is applied.
  
• From 3 (including) to 5.5 (not including), the equation Y=0⋅X+3 is applied.
  
• From 5.5 (including) to +∞, the equation Y=-0.5⋅X+2 is applied.
  

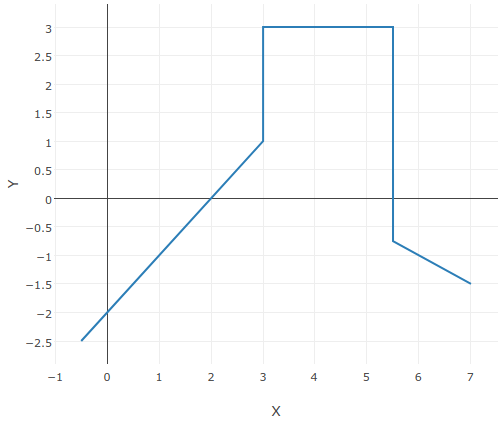
An example of a chart obtained when filling in the calculation table

a is a slope coefficient of the line

With a=0, the slope will be 0°; thus, the line will be parallel to the X-axis.
With a=1, the slope will be 45°; thus, the larger the coefficient, the closer the line will be to the Y-axis.
With a=-1, the slope will be −45 °; thus, negative values of this coefficient tilt the line down, and positive values — up.

An example of a chart of the Y=a⋅X line with different slope coefficients

b determines the displacement of the line along the Y-axis

When b=0, there is no displacement.
When b>0, the straight line is displaced upward relative to the X-axis.
When b<0, the displacement is downward.

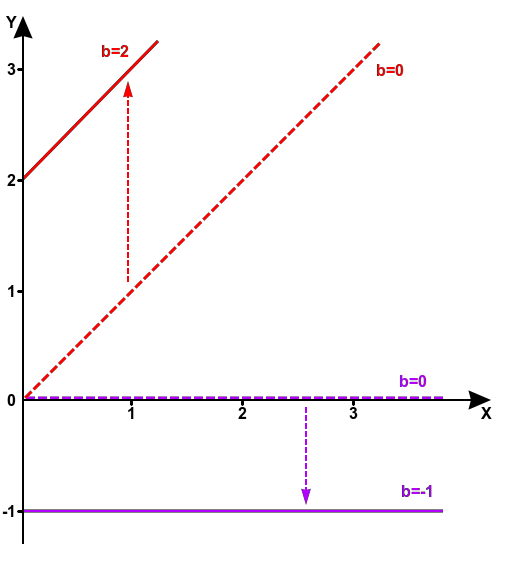
An example of lines with different displacements

Lower and upper bounds

Lower and upper bounds allow you to cut off erroneous sensor values according to a simple principle — if the value is outside the range between the lower and upper bounds, the sensor will display a dash (error).

Let’s consider an example with a fuel level sensor. Assume that parameter values from 3 to 250 correspond to fuel volumes from 0 liters to 100 liters. And the 0 or 255 values of the parameter mean errors that we want to exclude so that they are not interpreted as a realistic volume since the tank in the example cannot have less than 0 or more than 100 liters of fuel. For this example, you can propose a solution with the Apply after calculation option turned off:

There is also a solution with the Apply after calculation option enabled:

From the example, you can see that the Apply after calculation option affects which values the bounds apply to: if it is off, then the system filters out the values along the X-axis (the input values before applying the calculation table), and if it is enabled, then it filters out the values along the Y-axis (sensor values after applying the calculation table).

To visualize how the bounds work, consider another example in which the same bounds applied to the same straight line and the difference lies only in the Apply after calculation option, which significantly affects the result.

The lower bound equals 2, the upper bound equals 3, the Apply after calculation option is disabled

The lower bound equals 2, the upper bound equals 3, the Apply after calculation option is enabled

The principle of the calculation table operation

Sometimes, to understand the essence of a phenomenon, it's better to go backward. If we know the precise formula Y=f(X), which relates the input and output values over the entire range, then there is no need to use the calculation table. It's better to use the expression in the Parameter field instead. Let's consider such a case.

Suppose that an input value is related to an output value by the Y=0.5⋅X² formula.
Let's take adc3 as a parameter. To describe such a formula in Wialon, insert the following expression into the Parameter field: const0.5*adc3^const2

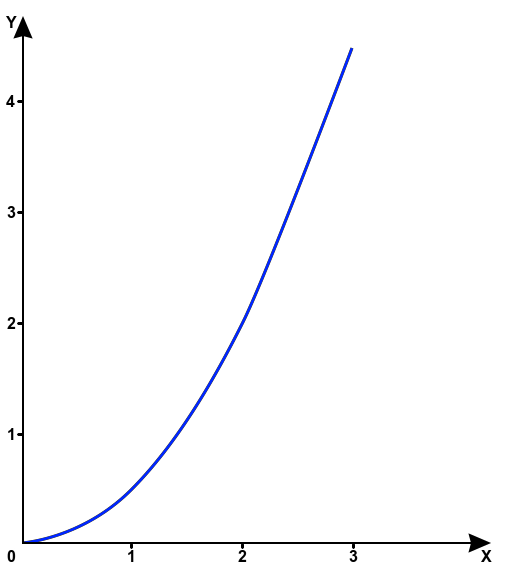
The chart of the Y=0.5⋅X² function

But what if we don't know the precise Y=f(X) formula? In this exact case, the calculation table will help us.

Suppose that we know the values of the measured value (it will be Y), and we can check what value the parameter will take in Wialon at those points (it will be X). Thus, you can get values, for example, at four points: (0; 0), (1; 0.5), (2; 2), (3; 4.5). Next, plot these points (X, Y) on the chart and connect them with red lines.

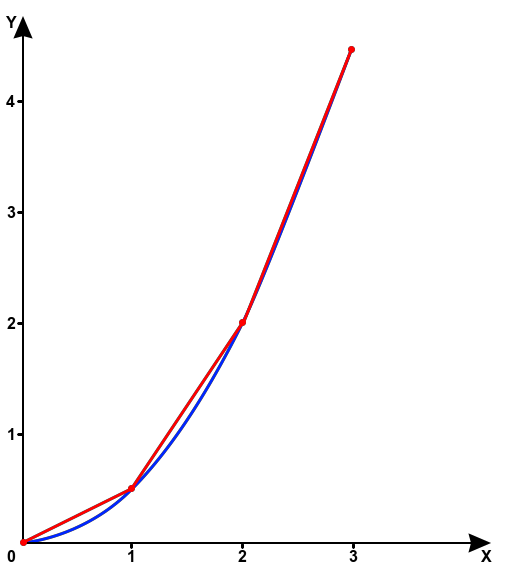
Reproduction of a part of the function Y=0.5⋅X² by lines built on four points

It is easy to see that the result is close to that obtained by the formula, but there are still differences. In some cases, this accuracy will be sufficient, but if it is not enough, you can measure values ​​at more points. The chart below shows an example for six points: (0; 0), (0.5; 0.125), (1; 0.5), (1.5; 1.125), (2; 2), (3; 4.5).

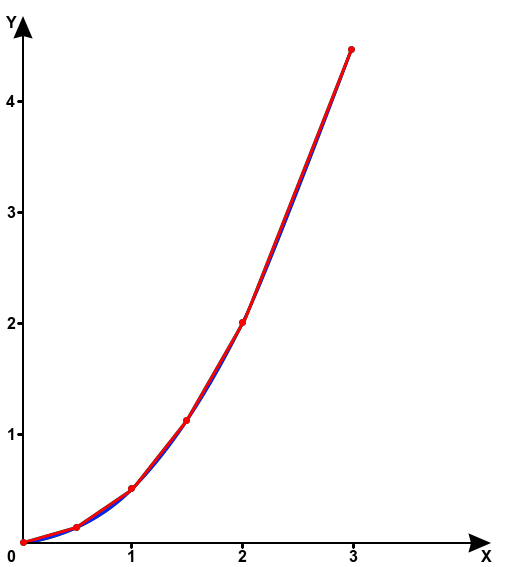
Reproduction of a part of the function Y=0.5⋅X² by lines built on six points

Rationale and use cases

In this section, we will consider several cases where the calculation table saves the day.

The curve that describes the relationship between X and Y can be quite complex.

For example, using a fuel level sensor requires calibrating the fuel tank, and the shape of the chart built according to the calibration table will depend on the geometry of the tank, which is never ideal (it may have roundings, dents, internal stiffeners, and so on).

The chart based on the calibration table with small steps between measurements

It is problematic to describe such dependence in one formula. An easier way to describe this curve is to break it down into intervals where it behaves roughly like a straight line and determine the formulas for those lines. You can do it using XY pairs.

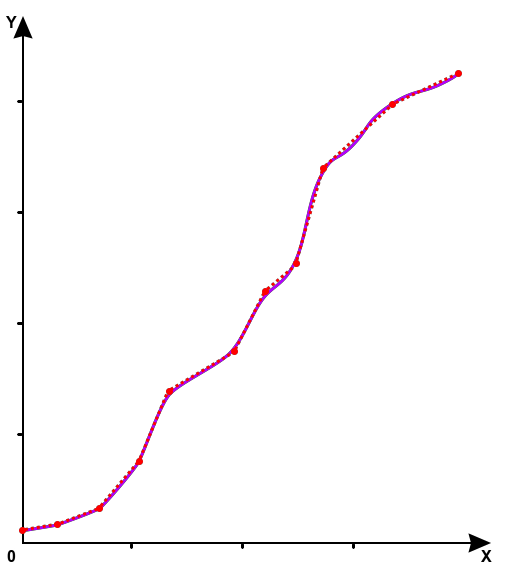
Reproduction of a complex curve by breaking it down into lines passing through eleven points

Also, sometimes the relationship between X and Y can vary over several intervals. To describe it, you need to use a system of several expressions, which cannot be done in the Parameter field in the sensor properties.

For example, some temperature sensors work as follows: X values in the range from 0 to 127 correspond to a positive temperature, and in the range from 128 to 255 — to a negative temperature. You will need a calculation table with two rows to handle such a case:

X=0; a=1; b=0
X=128; a=1; b=-256

The temperature chart where higher parameter values correspond to negative temperatures

Digital sensors are another prime example of a situation where the relationship between X and Y varies over several intervals. For example, an ignition sensor can be created based on a voltage parameter, and this requires two conditions taken into account: Y=0 when X<14 and Y=1 when X≥14. As we already know, this cannot be done using an expression in the sensor properties. But on the Calculation Table tab, this will require only two lines:

X=0; a=0; b=0
X=14; a=0; b=1

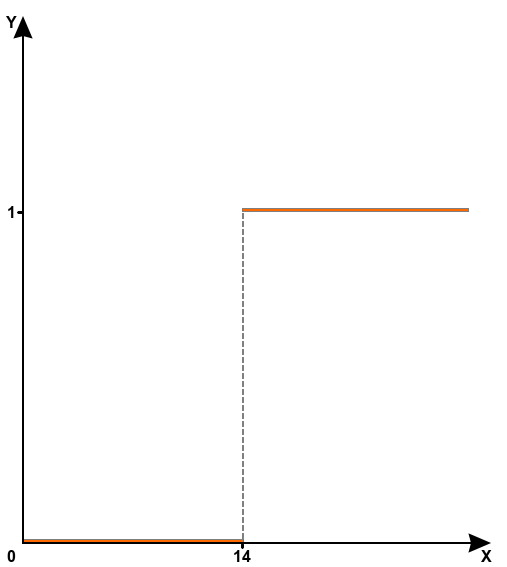
The ignition status chart depending on voltage

Oleg Zharkovsky,Customer Service Engineer 2023-02-21