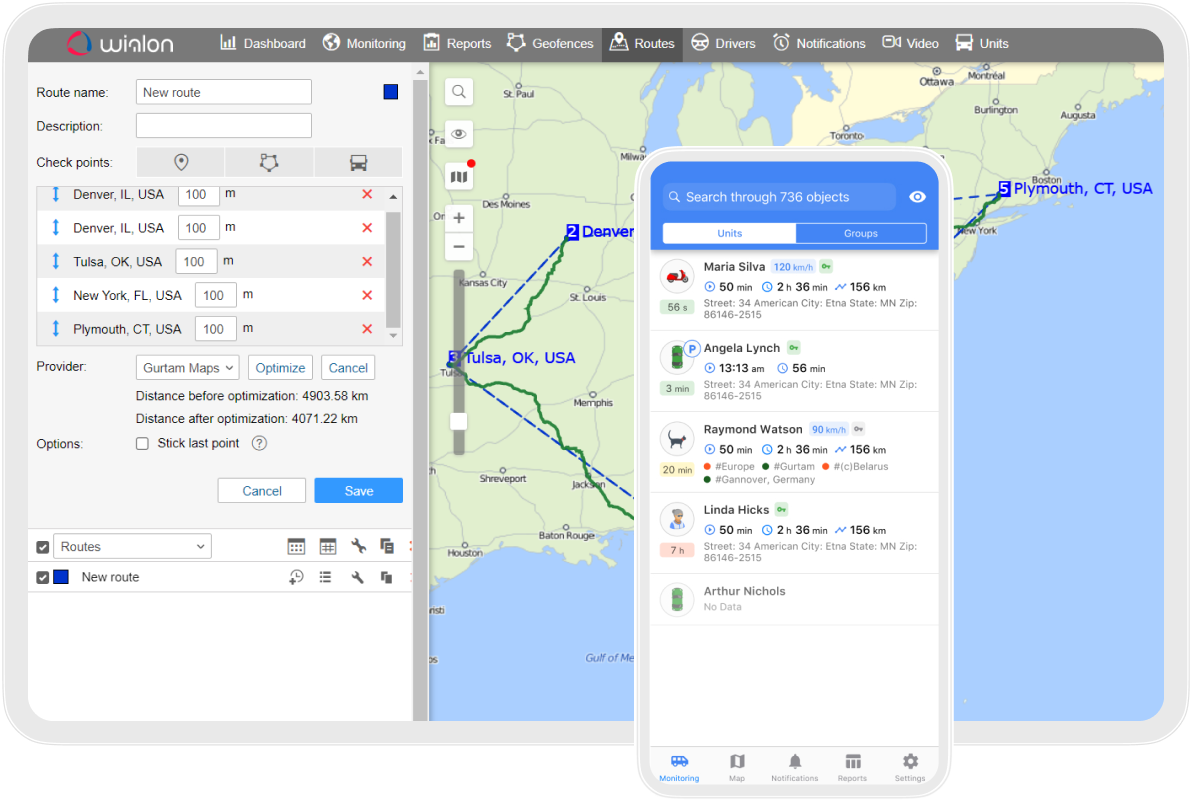
Wialon Hosting
Versión en la nube de Wialon, la solución definitiva para la digitalización de flotas, diseñada para optimizar las operaciones y mejorar la eficiencia de diversas flotas — desde automóviles y camiones hasta vehículos pesados y maquinaria.